
一方、スペインのLaLigaは、優勝チーム(Barcelona or Real Madrid)や上位に入るであろうチームが、容易く予想できることで有名です。
今回は、統計学の基礎であるローレンツ曲線を書くことで、上記2つのリーグを比較してみました。
1. はじめに
1.1. ローレンツ曲線とは
ローレンツ曲線は、以下のようなものです。
ローレンツ曲線(ローレンツきょくせん、英: Lorenz curve)とは、ある分布を持つ事象について、確率変数が取り得る値を変数とし、確率変数の値が与えられた変数の値を超えない範囲における確率変数と対応する確率の積の和(あるいは確率変数と確率密度関数の積の積分)を、その分布に対する確率変数の期待値で割って規格化ものとして与えられる関数の幾何学的な表現のことである。[Wikipediaより]
所得や資産が、どの程度、平等・不平等に配分されているかを示すのに用いられるようです。
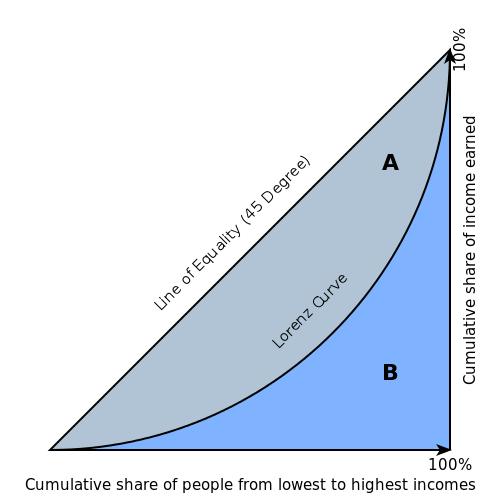
英語版Wikipediaにあった、以下の図がわかりやすいかもしれません。
この図のAが大きいほど、所得の格差が大きいとされます。
1.2. やりたいこと
ローレンツ曲線を描いて比較をしていきます。
- J1のクラブ間の総年俸の格差を図示
- LaLigaのクラブ間の総年俸の格差を図示
- J1とLaLigaの比較
2. J1のクラブ間格差
2.1. 概要
- 対象クラブ: J1 2018年 全18クラブ
- 利用するWebサイト: → https://www.soccer-money.net/team/in_team.php
2.2. ローレンツ曲線[J1]
(1) Webサイトから情報を取得
利用するWebサイトから、htmlを取得します。スクレイピングは、この本がわかりやすいです。
[amazonjs asin=”4774183679″ locale=”JP” title=”Pythonクローリング&スクレイピング -データ収集・解析のための実践開発ガイド-“]
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
import requests import lxml.html from urllib.request import urlopen from bs4 import BeautifulSoup import numpy as np import pandas as pd import matplotlib.pyplot as plt import csv import pandas as pd import matplotlib.pyplot as plt # ページの情報取得 url = "https://www.soccer-money.net/team/in_team.php" html = urlopen(url) encoding = html.info().get_content_charset(failobj="utf-8") html = html.read().decode(encoding) soup = BeautifulSoup(html, 'html.parser') table = soup.find_all('table')[1] |
↓の記事でやったのと、ほぼ同じです。

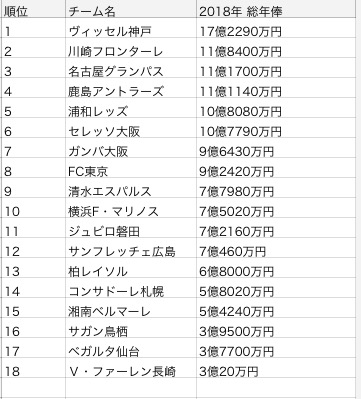
(2) csvに出力
先ほどのデータを整形し、csvファイルとして出力しましょう。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
# ヘッダー部分 csv_headers = [] for th in table.find_all('th'): csv_headers.append(th.text) n_headers = len(csv_headers) # 本体 csv_contents = [] for td in table.find_all('td'): csv_contents.append(td.text) # 出力 with open('J1_2018_salary.csv', 'w', newline='') as f: writer = csv.writer(f) writer.writerow(csv_headers) for i in range(0, len(csv_contents)): writer.writerow(csv_contents[i*n_headers:(i+1)*n_headers]) |
(3) ローレンツ曲線を描く
チーム毎の総年俸の格差を知りたいので、2つの累積相対度数を計算し、ローレンツ曲線を描きます。
- 総年俸について
- チーム数について
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
df = pd.read_csv("J1_2018_salary.csv") # 億とか万をどうにかする for i in range(0, len(df)): df.iloc[i, 2] = eval(df.iloc[i, 2].replace("億", "00000000+").replace("万", "0000").replace("円", "")) df = df.rename(columns={'2018年 総年俸': '2018年 総年俸(円)'}) # わかりやすいように昇順に df = df.sort_values('2018年 総年俸(円)') # 累積相対度数の列を追加 salary_list = np.array(np.cumsum(df['2018年 総年俸(円)'])) cumsum_salary_list = salary_list/max(salary_list) df['総年俸 累積相対度数'] = cumsum_salary_list teams_list = np.array(range(1, len(df)+1)) cumsum_teams_list = teams_list/max(teams_list) df['チーム数 累積相対度数'] = cumsum_teams_list # 見栄えがいいように、原点を追加 cumsum_salary_list = np.insert(cumsum_salary_list, 0, 0) cumsum_teams_list= np.insert(cumsum_teams_list, 0, 0) # ローレンツ曲線を描く plt.plot(cumsum_teams_list, cumsum_salary_list, label="Lorenz Curve") plt.xlim(-0.1, 1.1) plt.plot([0, 1], [0, 1], label="Line of Equality") plt.plot() plt.xlabel("n of Teams(%)") plt.ylabel("Total Salary(%)") plt.grid(True) plt.gca().set_aspect('equal', adjustable='box') plt.title("J1 League") plt.legend(loc="best") |
途中のDataFrameがこんな感じです。
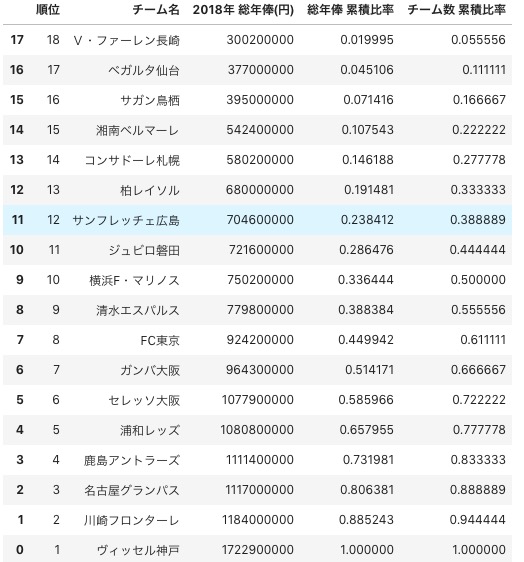
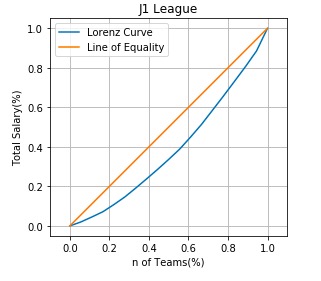
ローレンツ曲線はこのようになりました。三日月は細めですね。
3. LaLigaのクラブ間格差
3.1. 概要
- 対象クラブ: LaLiga ’17-’18 全20クラブ
- 利用するWebサイト: → https://www.totalsportek.com/money/la-liga-wage-bills/
3.2. ローレンツ曲線[LaLiga]
(1) csv
これまで同様に、Webサイトから情報をスクレイピングして、csvファイルにします。
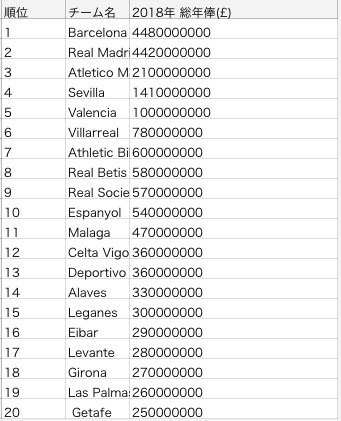
LaLigaの場合はこのような感じです。
利用したWebサイトには、「La Liga Clubs Wage Bill For 2017-18 Season」と書かれており、
総年俸と完全に一致しないかもしれませんが、気にせず使っていきます。単位は£です。
(2) ローレンツ曲線を描く
チーム毎の総年俸の格差を知りたいので、2つの累積相対度数を計算し、ローレンツ曲線を描きます。
J1のときと同様です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
laliga_df = pd.read_csv("LaLiga_2018.csv") laliga_df = laliga_df.sort_values('2018年 総年俸(£)') laliga_salary_list = np.array(np.cumsum(laliga_df['2018年 総年俸(£)'])) laliga_cumsum_salary_list = laliga_salary_list/max(laliga_salary_list) laliga_df['総年俸 累積相対度数'] = laliga_cumsum_salary_list laliga_teams_list = np.array(range(1, len(laliga_df)+1)) laliga_cumsum_teams_list = laliga_teams_list/max(laliga_teams_list) laliga_df['チーム数 累積相対度数'] = laliga_cumsum_teams_list laliga_cumsum_salary_list = np.insert(laliga_cumsum_salary_list, 0, 0) laliga_cumsum_teams_list= np.insert(laliga_cumsum_teams_list, 0, 0) plt.plot(laliga_cumsum_teams_list, laliga_cumsum_salary_list, label="Lorenz curve") plt.xlim(-0.1, 1.1) plt.plot([0, 1], [0, 1], label="diagonal line") plt.plot() plt.xlabel("n of teams(%)") plt.ylabel("tptal salary(%)") plt.title("La Liga") plt.gca().set_aspect('equal', adjustable='box') plt.grid(True) plt.legend(loc="best") |
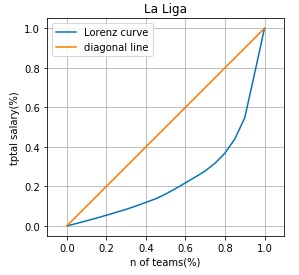
4. J1とLaLigaの比較
4.1. ローレンツ曲線
両リーグのローレンツ曲線を並べると、このようになります。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
plt.plot(cumsum_teams_list, cumsum_salary_list, label="Lorenz curve_J1", marker = '^') plt.plot(laliga_cumsum_teams_list, laliga_cumsum_salary_list, label="Lorenz curve_LaLiga", marker = 'o') plt.xlim(-0.1, 1.1) plt.plot([0, 1], [0, 1], label="Line of Equality") plt.plot() plt.xlabel("n of teams(%)") plt.ylabel("tptal salary(%)") plt.title("J1 and La Liga") plt.gca().set_aspect('equal', adjustable='box') plt.grid(True) plt.legend(loc="best") |
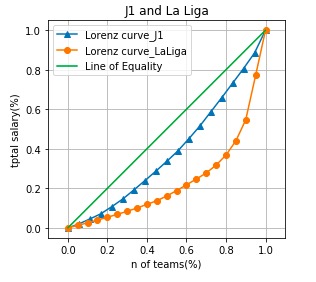
緑とオレンジの線から成る三日月型が大きいのがわかります。
つまり、LaLigaのほうが、クラブ間の格差が大きいことが、図示できました。
4.2. ジニ係数
ジニ係数というもので、不平等を数値化できます。
離散の場合は、以下の式を計算すればよいようです。
$$
Gini=\sum_{i}\sum_{j}\left| \frac{x_i-x_j}{2n^2 \overline{x}}\right|
$$
ローレンツ曲線と45度線の間の三日月型の面積を2で割ると算出できるみたいですね。
今回は、グラフで十分なので、計算しませんが、気になる方はぜひ。
5. 所感
- 統計学の基礎であるローレンツ曲線を書いた
- J1とLaLigaにおいて、クラブ間での不平等の度合いがわかった
- LaLigaのほうが、クラブ間の格差があった
[amazonjs asin=”4774183679″ locale=”JP” title=”Pythonクローリング&スクレイピング -データ収集・解析のための実践開発ガイド-“]
以上.



コメント