
懐かしいのでPythonで実装してみて、円周率(π)を近似してみます。図を描く練習にもなりました。
1. きっかけ
Pythonを勉強するにあたって、以下のような記事を目にしました。
GCIデータサイエンティスト育成講座の演習問題を解く Chapter2
学生時代に、そういえば習ったなあと思い、最近学習しているPythonで実装してみました。

2. モンテカルロ法とは
まずは、モンテカルロ法の説明です。
| モンテカルロ法 (モンテカルロほう、英: Monte Carlo method, MC) とはシミュレーションや数値計算を乱数を用いて行う手法の総称。元々は、中性子が物質中を動き回る様子を探るためにスタニスワフ・ウラムが考案しジョン・フォン・ノイマンにより命名された手法。カジノで有名な国家モナコ公国の4つの地区(カルティ)の1つであるモンテカルロから名付けられた。ランダム法とも呼ばれる。… [Wikipedia] |
これだと、乱数を用いたシミュレーションだということしかわかりません。
しかし、それ以上でもそれ以下でもありません。
詳しく知りたい方は以下を参照ください。わかりやすいと思います。
モンテカルロ法,乱数,および疑似乱数 杉田洋
3. モンテカルロ法による円周率(π)の近似
では、実際にモンテカルロ法でπを近似してみます。
0以上1以下の擬似乱数の組を生成します。それらを座標と見立てて平面にプロットしたとき、半径1の円の第一象限部分(扇形)の中に入る割合を求めていきます。
自分でも何言ってるかわからなくなってきたので、図をたくさん描いていきます。
3.1. 擬似乱数の生成
擬似乱数の生成にはnumpyを使います。
numpy.random.randを使えば、0以上1以下の一様乱数を生成できます。
|
1 2 3 4 |
import numpy as np import matplotlib.pylab as plt x = np.random.rand(10000) y = np.random.rand(10000) |
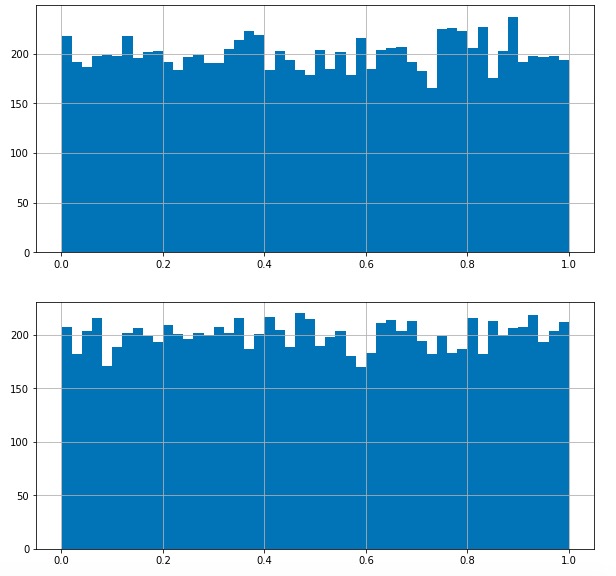
これで、1万個の点ができました。念の為、( x)と( y)の値についてヒストグラムを書いてみます。
上が( x)1で、下が( y)についてです。概ね、0以上1以下の範囲に一様に分布しています。
|
1 2 3 4 5 6 |
fig, axes = plt.subplots(2, 1, figsize=(10,10)) ax = axes.ravel() ax[0].hist(x, bins=50) ax[0].grid(True) ax[1].hist(y, bins=50) ax[1].grid(True) |
3.2. 扇形を図示してみる
問題となる扇形を以下に描きます。
描画には、matplotlibを使っていきます。
この図形の面積(青い部分)は、( π/4)であることに注意しましょう。
|
1 2 3 4 5 6 |
l = np.linspace(0, 1, 100) plt.plot(l, np.sqrt(1-l**2)) plt.gca().set_aspect('equal', adjustable='box') plt.xlabel("x") plt.ylabel("y") plt.fill_between(l,0,np.sqrt(1-l**2),facecolor='b',alpha=0.5) |
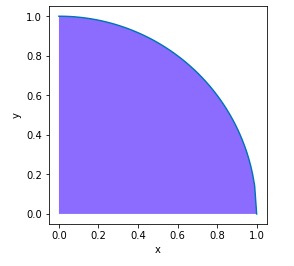
一方で、点(( x, y))が取りうる範囲は、1辺の長さが1の正方形ですので、
その面積は1となることにも注意します。
3.3. 扇形内の点と扇形外の点の数
点(( x, y))のうち、扇形の中にある点の個数を(n_{in})とします。
扇形の外にある点の個数は(n_{out})です。
格好いいコードがかけないので、単純に数え上げます。
扇形に入っているかどうかは、単純に原点とのユークリッド距離が1より小さいかどうかで判断します。
|
1 2 3 4 5 6 7 8 9 10 |
import math n_in = 0 n_out = 0 for i, j in zip(x, y): if math.hypot(i, j) < 1: n_in += 1 else: n_out += 1 print("内: {} 個".format(n_in)) print("外: {} 個".format(n_out)) |
![]()
3.4. ランダムな点を図示してみる
それぞれの個数はわかりましたが、僕の脳ではちょっとイメージしづらいので、
プロットしてみます。
|
1 2 3 4 5 6 7 |
plt.plot(l, np.sqrt(1-l**2)) plt.gca().set_aspect('equal', adjustable='box') plt.xlabel("x") plt.ylabel("y") plt.fill_between(l,0,np.sqrt(1-l**2),facecolor='b',alpha=0.5) plt.plot(x, y, 'o', markersize=0.4, label="random plot") plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left') |
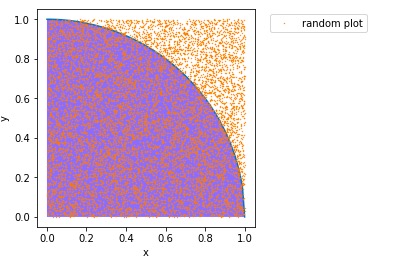
やっぱよくわかんないけど、満遍なくプロットされている気はします。
3.5. 円周率\(π\)を近似する
これまでの結果から、以下の式が成り立ちます。
$$π/4 : 1 \simeq n_{in} : n_{in} + n_{out}$$
従って、次のコードにより、円周率(π)の近似ができます。
|
1 2 |
pi_closed = 4 * n_in / (n_in + n_out) print("pi_closed: {:.3f}".format(pi_closed)) |
![]()
たかだか1万個の点でシミュレートしていますが、それなりに近い数字がでました。
点の数を10万個に増やしたときの結果も載せておきます。より3.14…に近い数字になっています。
![]()
4. やってみた感想
matplotlibでお絵描きするのが、とにかく楽しい!!!
以上



コメント